Sharp regression discontinuity with pymc models#
import causalpy as cp
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
seed = 42
df = cp.load_data("rd")
Linear, main-effects, and interaction model#
Note
The random_seed keyword argument for the PyMC sampler is not necessary. We use it here so that the results are reproducible.
result = cp.RegressionDiscontinuity(
df,
formula="y ~ 1 + x + treated + x:treated",
model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
treatment_threshold=0.5,
)
fig, ax = result.plot()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
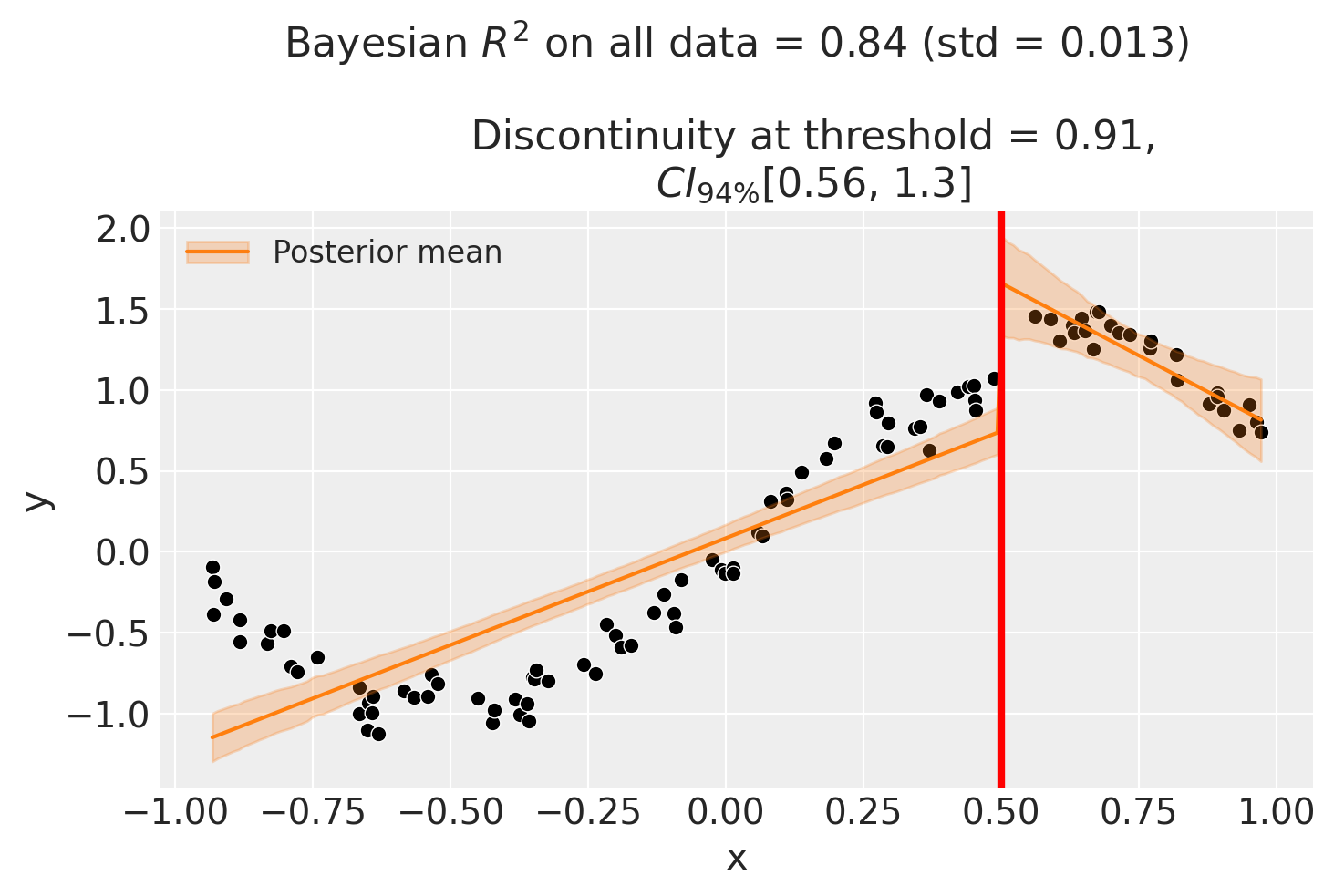
Though we can see that this does not give a good fit of the data almost certainly overestimates the discontinuity at threshold.
Using a bandwidth#
One way how we could deal with this is to use the bandwidth kwarg. This will only fit the model to data within a certain bandwidth of the threshold. If \(x\) is the running variable, then the model will only be fitted to data where \(threshold - bandwidth \le x \le threshold + bandwidth\).
result = cp.RegressionDiscontinuity(
df,
formula="y ~ 1 + x + treated + x:treated",
model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
treatment_threshold=0.5,
bandwidth=0.3,
)
fig, ax = result.plot()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 3 seconds.
There were 3 divergences after tuning. Increase `target_accept` or reparameterize.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
We could even go crazy and just fit intercepts for the data close to the threshold. But clearly this will involve more estimation error as we are using less data.
result = cp.RegressionDiscontinuity(
df,
formula="y ~ 1 + treated",
model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
treatment_threshold=0.5,
bandwidth=0.2,
)
fig, ax = result.plot()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Using basis splines#
Though it could arguably be better to fit with a more complex model, fit example a spline. This allows us to use all of the data, and (depending on the situation) maybe give a better fit.
result = cp.RegressionDiscontinuity(
df,
formula="y ~ 1 + bs(x, df=6) + treated",
model=cp.pymc_models.LinearRegression(sample_kwargs={"random_seed": seed}),
treatment_threshold=0.5,
)
fig, ax = result.plot()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, y_hat_sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Sampling: [beta, y_hat, y_hat_sigma]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
Sampling: [y_hat]
As with all of the models in this notebook, we can ask for a summary of the model coefficients.
result.summary()
Difference in Differences experiment
Formula: y ~ 1 + bs(x, df=6) + treated
Running variable: x
Threshold on running variable: 0.5
Results:
Discontinuity at threshold = 0.41$CI_{94\%}$[0.23, 0.59]
Model coefficients:
Intercept -0.23, 94% HDI [-0.32, -0.14]
treated[T.True] 0.41, 94% HDI [0.23, 0.59]
bs(x, df=6)[0] -0.59, 94% HDI [-0.79, -0.41]
bs(x, df=6)[1] -1.1, 94% HDI [-1.2, -0.93]
bs(x, df=6)[2] 0.28, 94% HDI [0.11, 0.43]
bs(x, df=6)[3] 1.7, 94% HDI [1.5, 1.8]
bs(x, df=6)[4] 1, 94% HDI [0.67, 1.4]
bs(x, df=6)[5] 0.57, 94% HDI [0.37, 0.76]
y_hat_sigma 0.1, 94% HDI [0.089, 0.12]
Effect Summary Reporting#
For decision-making, you often need a concise summary of the causal effect. The effect_summary() method provides a decision-ready report with key statistics. Note that for Regression Discontinuity, the effect is a single scalar (the discontinuity at the threshold), similar to Difference-in-Differences.
# Generate effect summary
stats = result.effect_summary()
stats.table
| mean | median | hdi_lower | hdi_upper | p_gt_0 | |
|---|---|---|---|---|---|
| discontinuity | 0.408901 | 0.406947 | 0.229298 | 0.595095 | 1.0 |
print(stats.text)
The discontinuity at threshold was 0.41 (95% HDI [0.23, 0.60]), with a posterior probability of an increase of 1.000.
You can customize the summary with different directions and ROPE thresholds:
Direction: Test for increase, decrease, or two-sided effect
Alpha: Set the HDI confidence level (default 95%)
ROPE: Specify a minimal effect size threshold
# Example: Two-sided test with ROPE
stats = result.effect_summary(
direction="two-sided",
alpha=0.05,
min_effect=0.2, # Region of Practical Equivalence
)
stats.table
| mean | median | hdi_lower | hdi_upper | p_two_sided | prob_of_effect | p_rope | |
|---|---|---|---|---|---|---|---|
| discontinuity | 0.408901 | 0.406947 | 0.229298 | 0.595095 | 0.0 | 1.0 | 0.98875 |
print("\n" + stats.text)
The discontinuity at threshold was 0.41 (95% HDI [0.23, 0.60]), with a posterior probability of an effect of 1.000.
